TX Pulse Shaping & Matched Filters

Est. read time: 1 minute | Last updated: January 27, 2026 by John Gentile

Contents

Matched Filtering
Derivative Matched Filter (DMF)
References

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from rfproto import filter, modulation, plot, sig_gen

Matched Filtering

The why (bandwidth and power amplifiers) -> https://dsp.stackexchange.com/questions/41130/envelope-behavior-difference-between-qpsk-oqpsk-and-pi-4-qpsk
https://en.wikipedia.org/wiki/Raised-cosine_filter

# CCSDS OQPSK SRRC rolloff=0.5: https://public.ccsds.org/Pubs/413x0g3e1.pdf
rrc_test = filter.RootRaisedCosine(17.225e6, 7.5e6, 0.5, 63)
# The matched filter is a time-reversed and conjugated version of the signal
# NOTE: this is moot for a uniform, real filter...
rrc_mf = np.conj(rrc_test[::-1])
plot.filter_coefficients(rrc_mf)
plt.show()

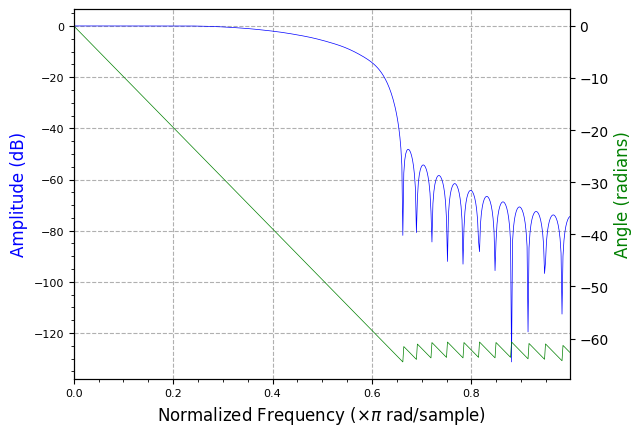
plot.filter_response(rrc_mf)
plt.show()

png

# simulate random binary input values
num_symbols  = 2400
num_disp_sym = 16
sym_rate     = 1e6 # Baseband symbol rate
# Generate random QPSK symbols
rand_symbols = np.random.randint(0, 4, num_symbols)

L  = 4               # Upsample ratio (Samples per Symbol)
fs = L * sym_rate    # Output sample rate (Hz)

rolloff          = 0.25 # Alpha of RRC
num_filt_symbols = 6    # Symbol length of RRC matched filter

qpsk_tx_filtered = sig_gen.gen_mod_signal(
    "QPSK",
    rand_symbols,
    fs,
    sym_rate,
    "RRC",
    rolloff,
    num_filt_symbols,
)

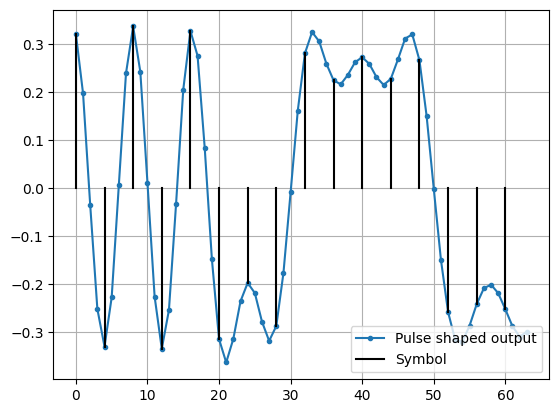
# Show time domain aspects of interpolation & pulse-shapinp
fig, ax = plt.subplots()
ax.plot(np.real(qpsk_tx_filtered[:num_disp_sym * L]), '.-', label='Pulse shaped output')
num_taps = 64
for i in range(num_disp_sym):
    if not i:
        plt.plot([i*L,i*L], [0, np.real(qpsk_tx_filtered[i*L])], color='k', label='Symbol')
    else:
        plt.plot([i*L,i*L], [0, np.real(qpsk_tx_filtered[i*L])], color='k')
plt.grid(True)
plt.legend()
plt.show()

png

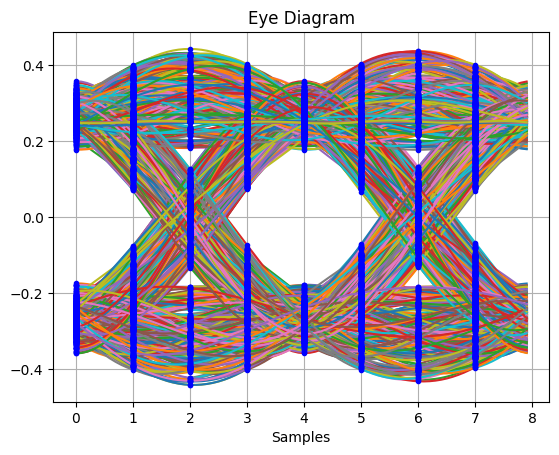
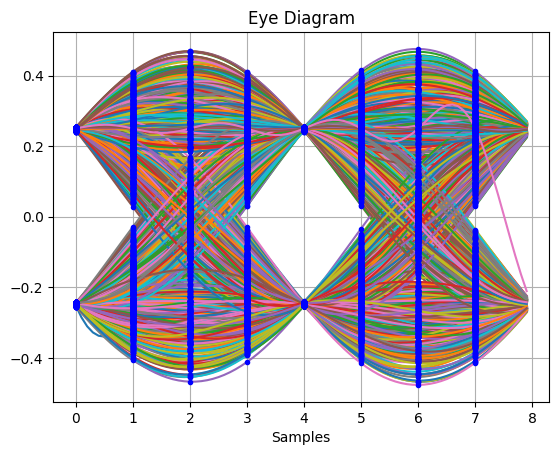
_,_ = plot.eye(qpsk_tx_filtered.real, L)
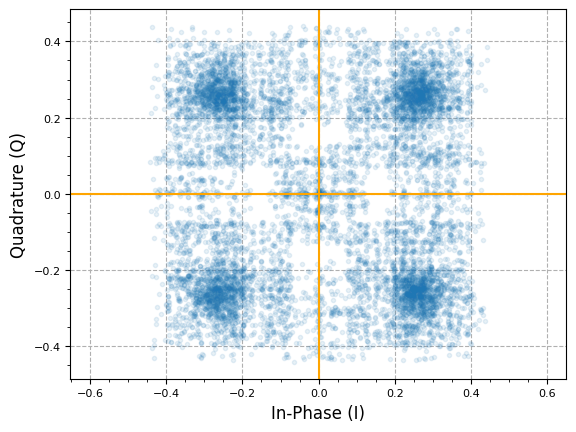
plot.IQ(qpsk_tx_filtered, alpha=0.1)
plt.show()

png

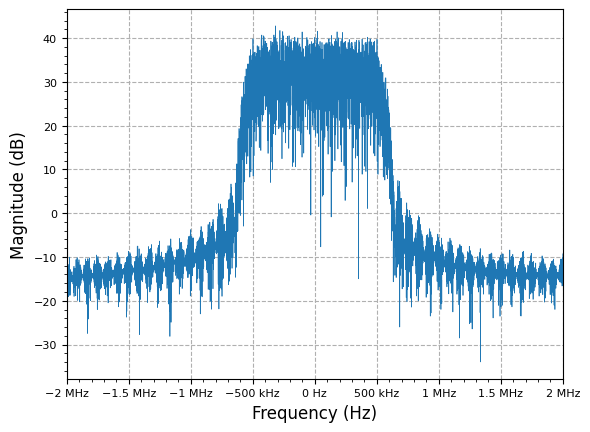
plot.spec_an(qpsk_tx_filtered, fs=fs, fft_shift=True, show_SFDR=False, y_unit="dB")
plt.show()

png

# Pass transmitted waveform through same RRC (matched filter)
rrc_coef = filter.RootRaisedCosine(L * sym_rate, sym_rate, rolloff, 2 * num_filt_symbols * L + 1)
rx_shaped = signal.lfilter(rrc_coef, 1, qpsk_tx_filtered)
# don't plot begining samples while starting filter convolution process
transient = (len(rrc_coef)//2 + 1) * L
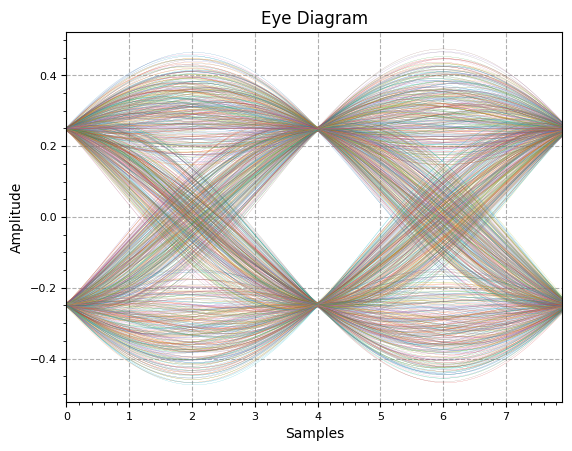
_,_ = plot.eye(rx_shaped.real[transient:], L )

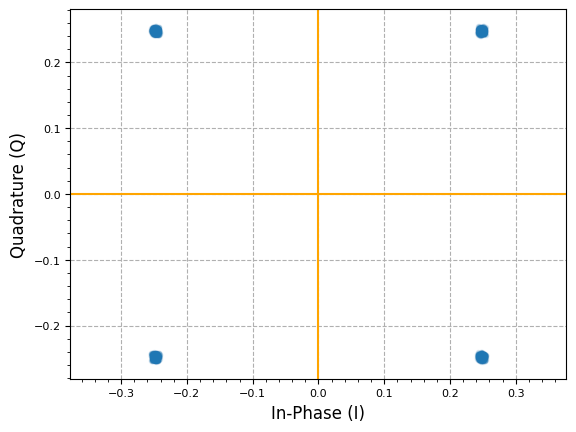
# adjust for best EVM, similar to slicer
timing_offset = 4
plot.IQ(rx_shaped[transient + timing_offset::4], alpha=0.1)
plt.show()

png

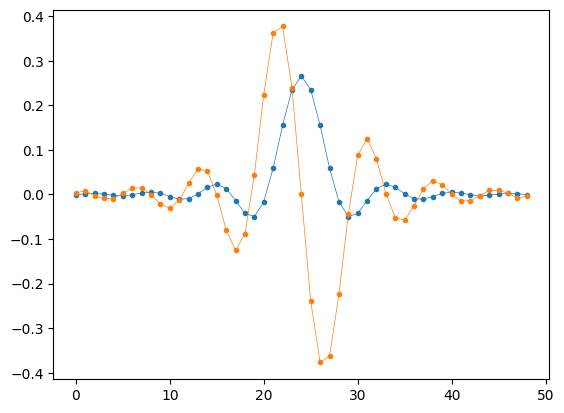
Derivative Matched Filter (DMF)

n_fft = 2048
freq_bins = np.linspace(-L/2, L/2, n_fft)

H_rrc = np.fft.fft(rrc_coef, n_fft)
H_dmf = 1j* 2 * np.pi * np.fft.fftfreq(n_fft) * L * H_rrc

dmf_full = np.fft.ifft(H_dmf)
dmf = np.real(dmf_full[:len(rrc_coef)])
#dmf /= np.max(np.abs(dmf))

Y_rrc = 20.0 * np.log10(np.abs(np.fft.fftshift(H_rrc)))
Y_dmf = 20.0 * np.log10(np.abs(np.fft.fftshift(np.fft.fft(dmf, n_fft))))

plt.figure()
plt.plot(rrc_coef, '.-', linewidth=0.5)
plt.plot(dmf, '.-', linewidth=0.5)
plt.show()

plt.figure()
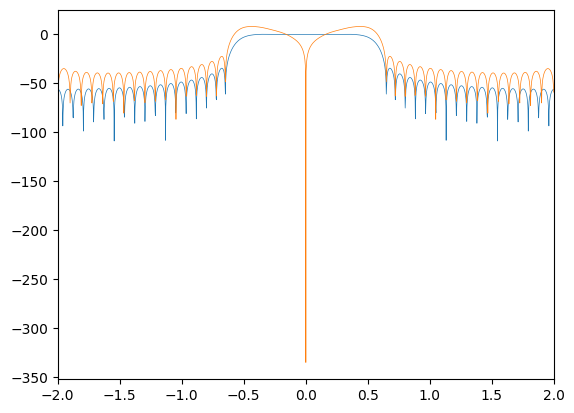
plt.plot(freq_bins, Y_rrc, linewidth=0.5)
plt.plot(freq_bins, Y_dmf, linewidth=0.5)
plt.margins(x=0)
plt.show()

png

TX Pulse Shaping & Matched Filters

Matched Filtering

Derivative Matched Filter (DMF)

References