Est. read time: 1 minute | Last updated: July 15, 2025 by John Gentile

Contents

Open In Colab

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from rfproto import impairments, plot, sig_gen

Fourier-Based Analysis Methods

Short-Time Fourier Transforms (STFTs)

# simulate random binary input values
num_symbols  = 2**15
num_disp_sym = 16
sym_rate     = 1e6 # Baseband symbol rate
# Generate random QPSK symbols
rand_symbols = np.random.randint(0, 4, num_symbols)

L  = 4               # Upsample ratio (Samples per Symbol)
fs = L * sym_rate    # Output sample rate (Hz)

rolloff          = 0.25 # Alpha of RRC
num_filt_symbols = 6    # Symbol length of RRC matched filter

qpsk_tx_filtered = sig_gen.gen_mod_signal(
    "QPSK",
    rand_symbols,
    fs,
    sym_rate,
    "RRC",
    rolloff,
    num_filt_symbols,
)

noise = impairments.awgn(-34, len(qpsk_tx_filtered))
qpsk_sig = qpsk_tx_filtered + noise

w = signal.windows.hamming(31)
plot.spectrogram(qpsk_sig, w, 2048, 64, 34)

png

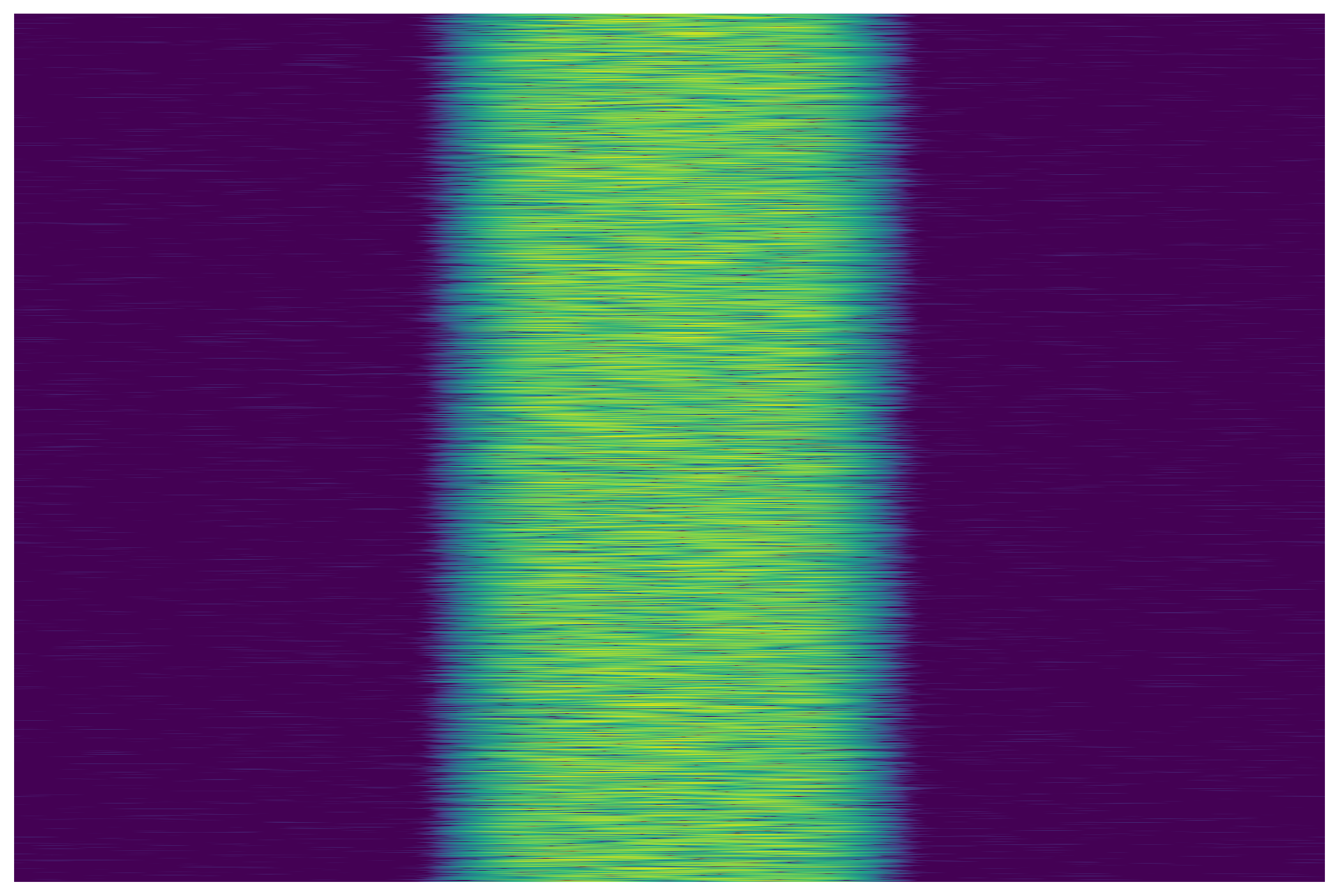
Polyphase Filter Bank (PFB) Channelizers

For higher quality spectral analysis than STFT methods, one should use a filterbank approach instead of a windowed FFT. Put simply, the STFT approaches use a single multiplication per sample at the input of the FFT- a channelizer uses a polyphase filter for each input. With PFB filtering, much better spectral separation is achieved between the FFT bins compared to just windowing.

For more info, see the Multirate DSP page on PFB Channelizers.

References



Maintained by John Gentile • Found a problem on this site? File an Issue
This work is licensed under a Creative Commons Attribution 4.0 International License.